Induksi Matematika

Induksi matematika merupakan pembuktian deduktif, meski namanya induksi. Induksi matematika atau disebut juga induksi lengkap sering dipergunakan untuk pernyataan-pernyataan yang menyangkut bilangan-bilangan asli.
Pembuktian cara induksi matematika ingin membuktikan bahwa teori atau sifat itu benar untuk semua bilangan asli atau semua bilangan dalam himpunan bagiannya. Caranya ialah dengan menunjukkan bahwa sifat itu benar untuk n = 1 (atau S(1) adalah benar), kemudian ditunjukkan bahwa bila sifat itu benar untuk n = k (bila S(k) benar) menyebabkan sifat itu benar untuk n = k + 1 (atau S(k + 1) benar).
Contoh soal:
Buktikan bahwa jumlah n bilangan ganjil pertama adalah n².
Persamaan yang perlu dibuktikan:

Langkah pembuktian pertama:
untuk , benar bahwa
Langkah pembuktian kedua:
andaikan benar untuk n = k, yaitu

, maka akan dibuktikan benar pula untuk n = k + 1, yaitu

sekarang sederhanakan persamaan pada sisi kiri dengan mengingat bahwa k² = 1 + 3 + 5 + ... + 2k − 1 sesuai dengan pengandaian awal

kemudian padankan bentuk sederhana tadi dengan sebelah kanan

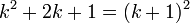, ingat bahwa (k + 1)² = k² + 2k + 1

(terbukti benar)

Kesimpulan:
Jadi, S(n) benar untuk semua bilangan asli karena memenuhi kedua langkah pembuktian.
 Induksi Matematika merupakan suatu teknik yang dikembangkan untuk membuktikan pernyataan  Induksi Matematika digunakan untuk mengecek hasil proses yang terjadi secara berulang sesuai dengan pola tertentu  Indukasi Matematika digunakan untuk membuktikan universal statements  n  A S(n) dengan A  N dan N adalah himpunan bilangan positif atau himpunan bilangan asli.  S(n) adalah fungsi propositional

sumber : http://id.wikipedia.org/wiki/Induksi_matematika